This page contains implementation of a method for mapping word sense embeddings to synsets, descibed in the paper "Best of Both Worlds: Making Word Sense Embeddings Interpretable". Word sense embeddings represent a word sense as a low-dimensional numeric vector. While this representation is potentially useful for NLP applications, its interpretability is inherently limited. We propose a simple technique that improves interpretability of sense vectors by mapping them to synsets of a lexical resource. Our experiments with AdaGram sense embeddings and BabelNet synsets show that it is possible to retrieve synsets that correspond to automatically learned sense vectors with Precision of 0.87, Recall of 0.42 and AUC of 0.78.

Motivation: Two Worlds of Lexical Semantics

Two key approaches to modelling semantics of lexical units are lexicography and statistical corpus analysis. In the first approach, a human explicitly encodes lexical-semantic knowledge, usually in the form of synsets, typed relations between synsets and sense definitions. A prominent examples of this approach is Princeton WordNet. The second approach makes use of text corpora to extract relations between words and feature representations of words and senses. These methods are trying to avoid manual work as much as possible. Prominent examples of this group of methods are distributional models and word embeddings.

The strongest side of lexical-semantic resources is their interpretability -- they are entirely human-readable and drawn distinctions are motivated by lexicographic or psychological considerations. On the downside, these WordNet-like resources are expensive to create, and it is not easy to adapt them to a given domain of interest. On the other hand, corpus-driven approaches are strong at adaptivity -- they can be re-trained on a new corpus, thus naturally adapting to the domain at hand. If fitted with a word sense induction algorithm, corpus-driven approaches can also discover new senses. However, the representations they deliver are often not matching the standards of lexicography, and they rather distinguish word usages than senses. Moreover, especially for dense vector representations as present in latent vector spaces and word embeddings, the representations are barely interpretable.

The main motivation of our method is to close this gap between interpretability and adaptivity of lexical-semantic models by linking word sense embeddings to synsets. We demonstrate usage of our method on a combination of BabelNet and AdaGram sense embeddings. However the approach can be straightforwardly applied to any WordNet-like resource and word sense embeddings.

Method: Linking Embeddings to Synsets

Our matching technique takes as input a trained word sense embeddings model, a set of synsets from a lexical resource and outputs a mapping from sense embeddings to synsets of the lexical resource. The method includes four steps. First, we convert word sense embeddings to a lexicalized representation and perform alignment via word overlap. Second we build a bag-of-word (BoW) representation of synsets. Third, we build a bag-of-word representation of sense embeddings. Finally, we measure similarity of senses and link most similar vector-synset pairs. The following figure desribes overview of the overall procedure:

Schema

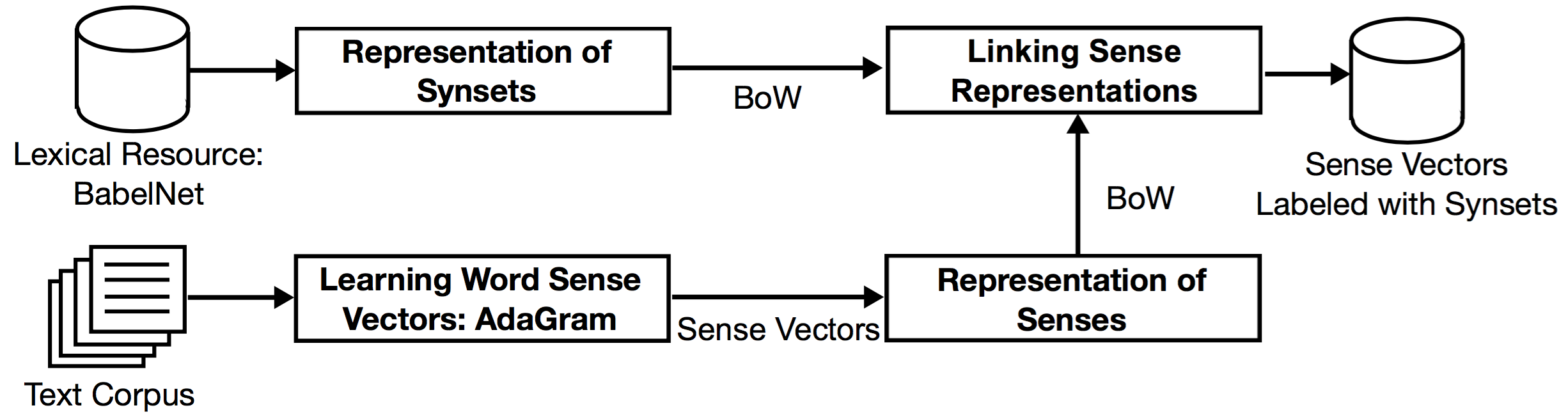
Citation Information

If you would like to refer to the vec2synset approach please use this citation (PDF):

@InProceedings{PANCHENKO16.625,
  author = {Alexander Panchenko},
  title = {Best of Both Worlds: Making Word Sense Embeddings Interpretable},
  booktitle = {Proceedings of the Tenth International Conference on Language Resources and Evaluation (LREC 2016)},
  year = {2016},
  month = {may},
  date = {23-28},
  location = {Portorož, Slovenia},
  editor = {Nicoletta Calzolari (Conference Chair) and Khalid Choukri and Thierry Declerck and Marko Grobelnik and Bente Maegaard and Joseph Mariani and Asuncion Moreno and Jan Odijk and Stelios Piperidis},
  publisher = {European Language Resources Association (ELRA)},
  address = {Paris, France},
  isbn = {978-2-9517408-9-1},
 }

Downloads: Reproducing Results